Das Haus vom Nikolaus und was Mathematik damit zu tun hat
Fast jeder hat es schon einmal gezeichnet oder zumindest versucht: das berühmte Haus vom Nikolaus.
Ein Quadrat, ein Kreuz, ein Dach und die große Herausforderung: Es soll mit einem einzigen Strich entstehen, ohne den Stift abzusetzen und keine Linie doppelt zu ziehen.
Klingt simpel? Ist es nicht. Denn tatsächlich steckt hinter diesem kleinen Rätsel ein Stück Mathematikgeschichte, und zwar mit einem der bekanntesten Namen überhaupt: Leonhard Euler.
Schritt für Schritt zum Haus vom Nikolaus
Am Anfang steht ein einfacher Strich. Die Basis des Hauses.
Noch nichts Besonderes, könnte man denken.
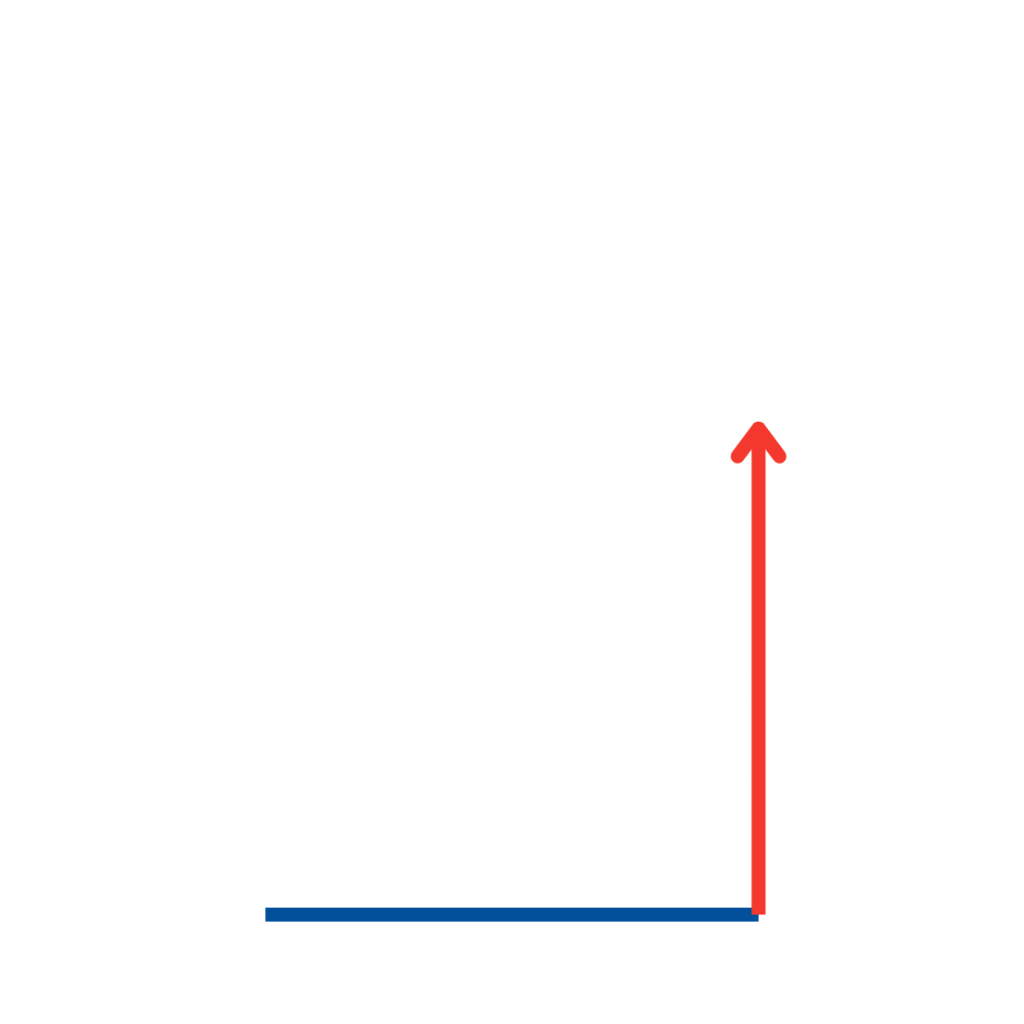
Mit der nächsten Linie entsteht die erste Seitenwand. Das Haus nimmt langsam Form an und auch die mathematische Herausforderung wächst mit jedem Schritt.
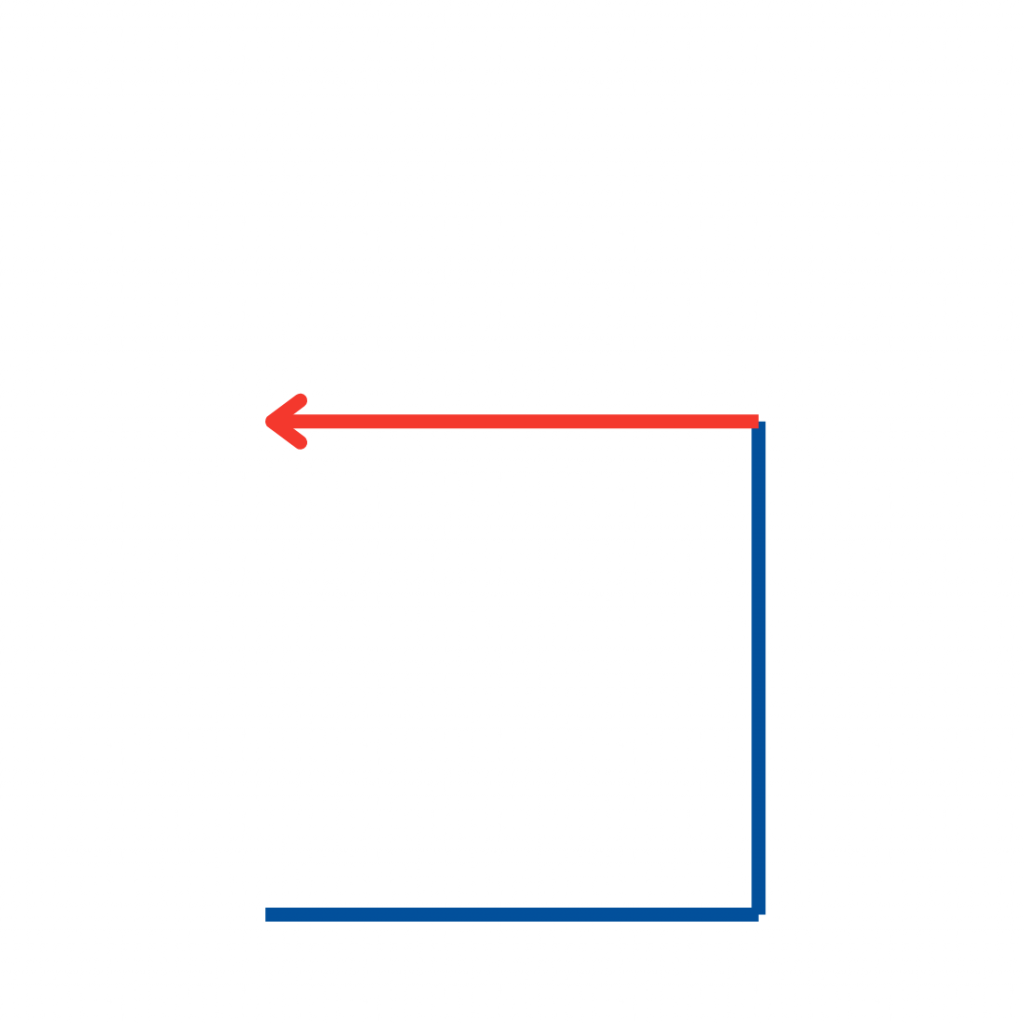
Jetzt geht es nach links: Das Dach wird gezeichnet.
Ein klarer, einfacher Zug, aber die Figur beginnt, sich zu verzweigen.
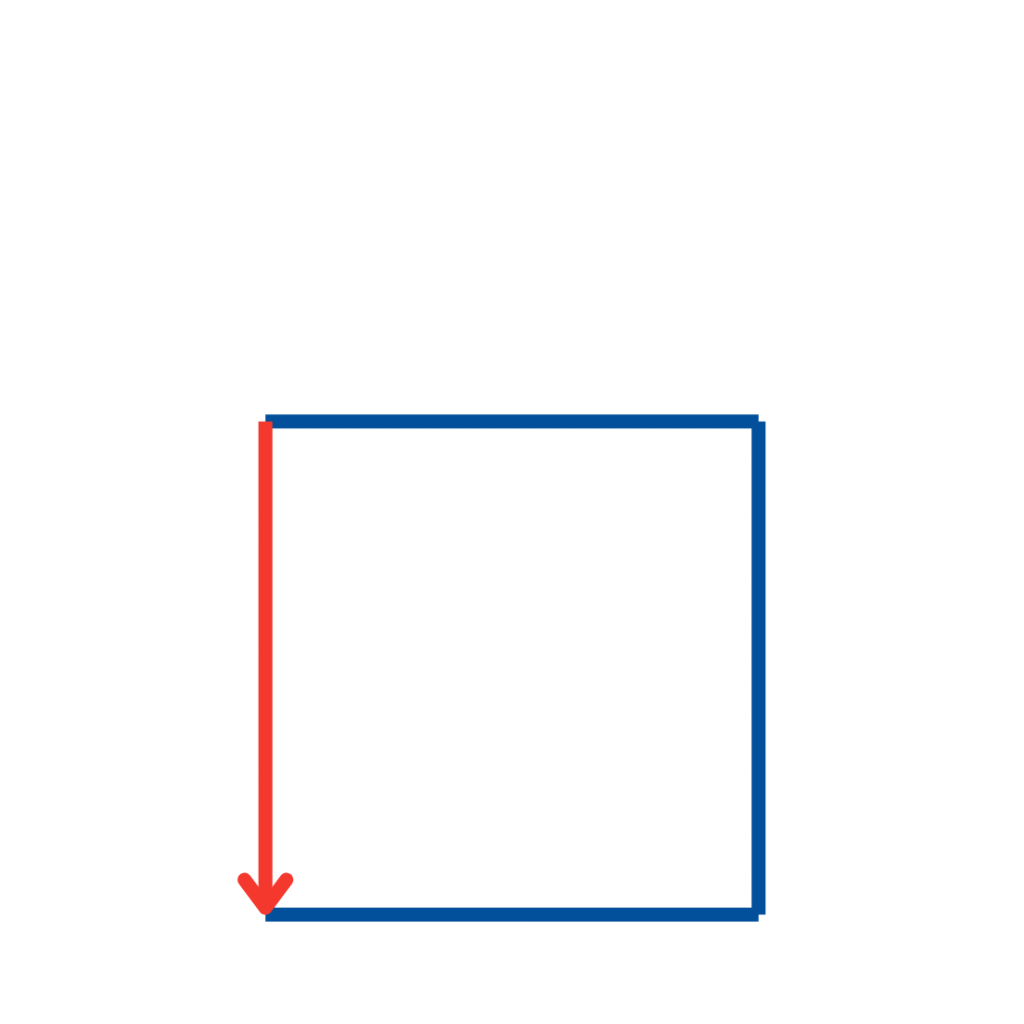
Mit der zweiten Seitenwand wird das Fundament vollständig.
Vier Punkte sind jetzt verbunden, aber der Weg durch die Linien ist noch nicht zu Ende.
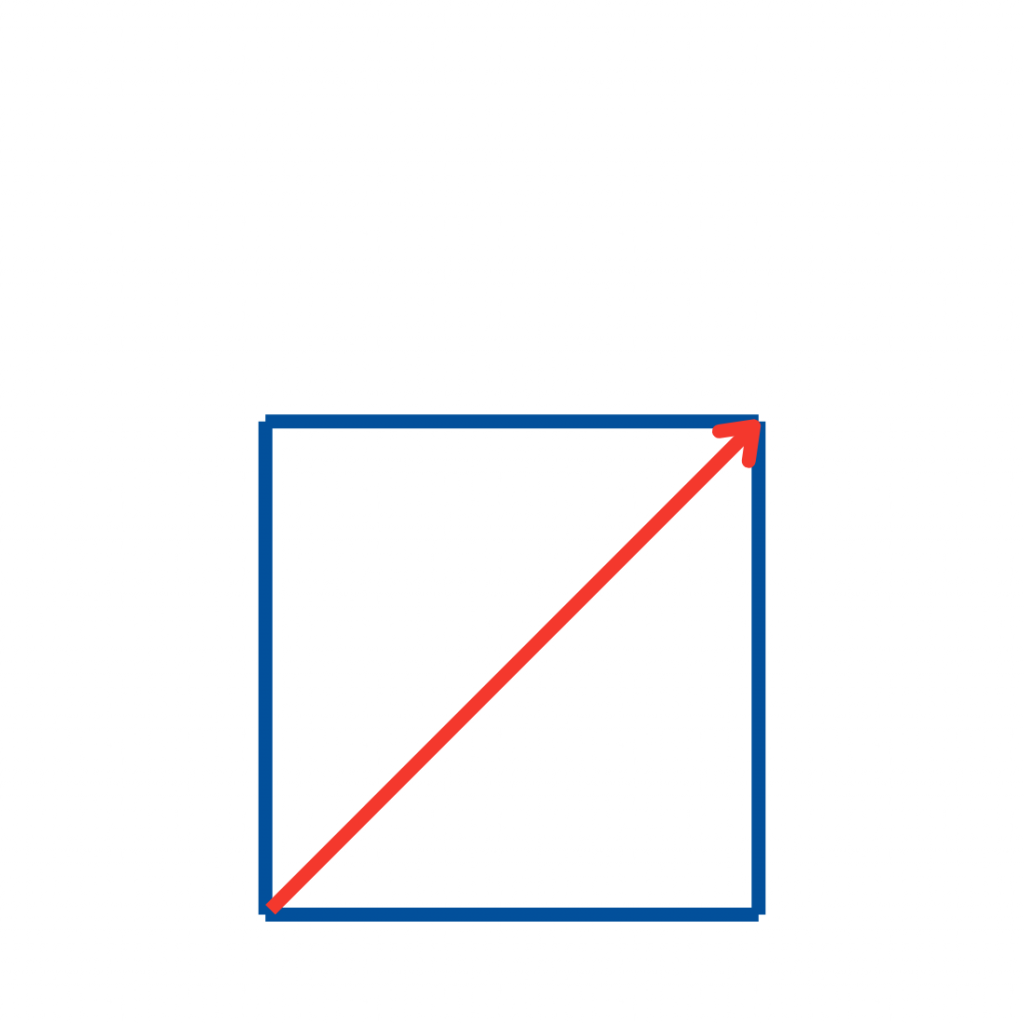
Die erste Diagonale beginnt das typische Kreuz in der Mitte.
Hier wird klar: Die Linien beginnen, sich zu überschneiden. Das ist der Kern des Rätsels.
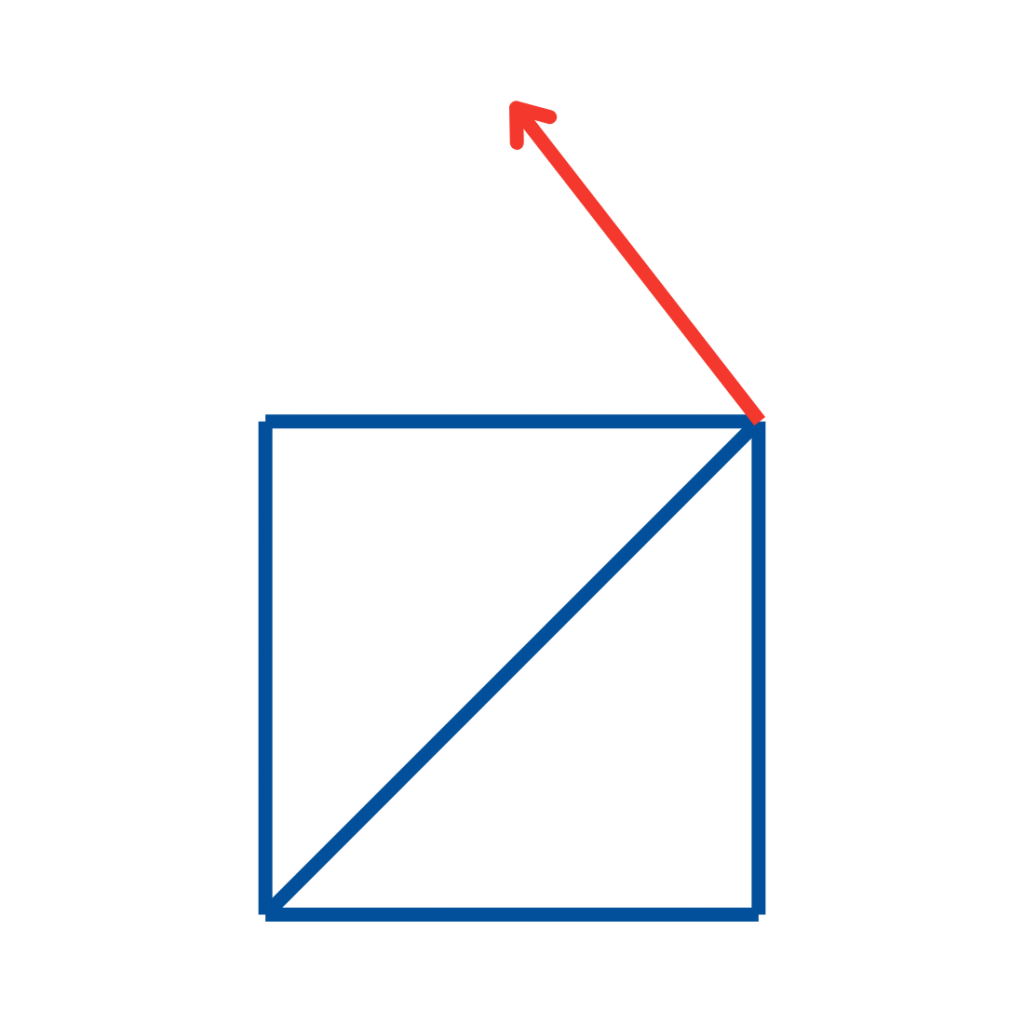
Jetzt kommt das Dach hinzu. Elegant, aber nicht ohne Risiko:
Ein falscher Zug, und man müsste eine Linie doppelt zeichnen.
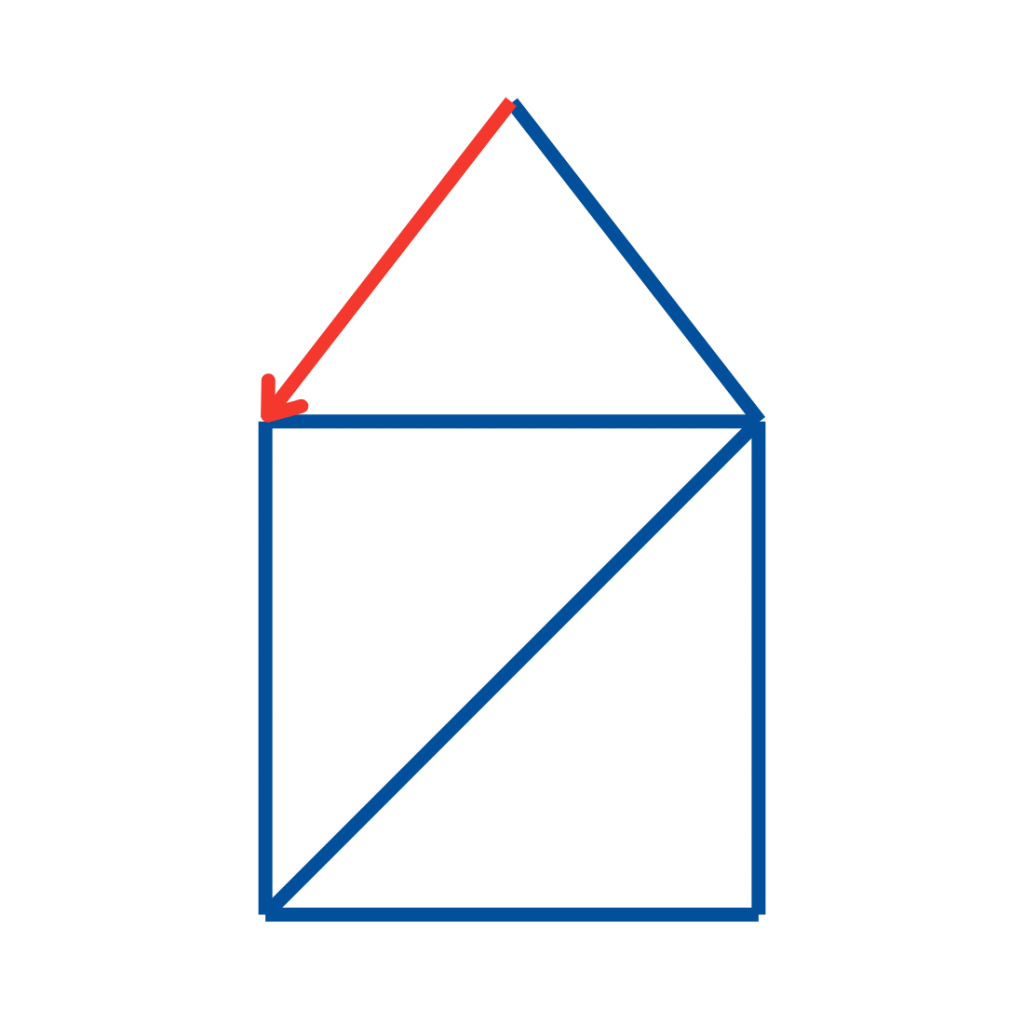
Mit der zweiten Dachhälfte steht das Haus endlich komplett.
Aber war das schon alles? Noch nicht, jetzt kommt die zweite Diagonale.
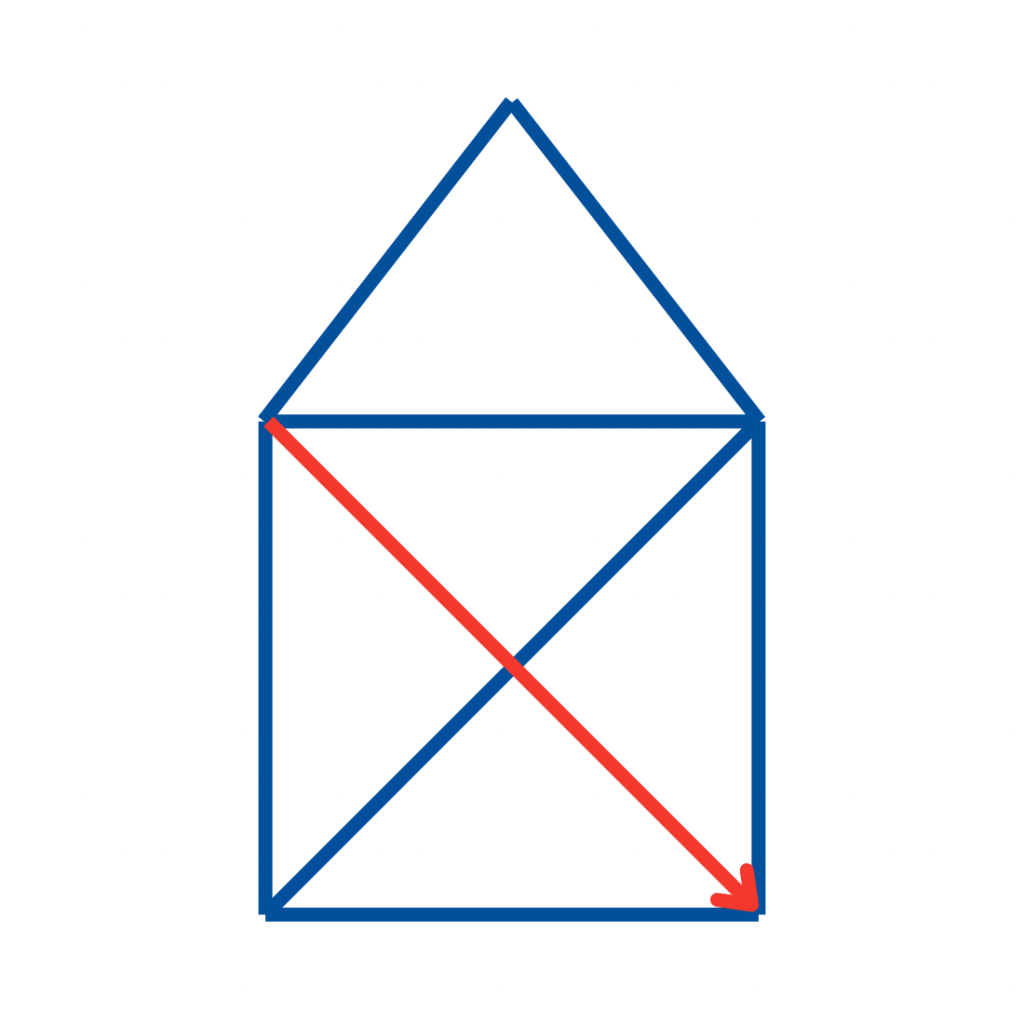
Die zweite Diagonale schließt die Figur. Das Haus ist fertig gezeichnet und wer es ohne Absetzen geschafft hat, hat einen sogenannten Eulerweg gefunden.
Das Ergebnis: ein vollständiges Haus, klar, strukturiert und – typisch Mathematik – vollkommen logisch aufgebaut.
Der Trick mit den Ecken
Jetzt, wo alle Linien gezeichnet sind, und zwar ohne sich zu doppeln oder zu überlagern, zeigt sich, warum das Haus vom Nikolaus mathematisch so spannend ist.
Es besteht aus fünf Punkten (Knoten), das sind die vier Hausecken und die Dachspitze, und acht Linien (Kanten), das sind die vier Seiten des Quadrats, die beiden Dachkanten und die beiden Diagonalen im Inneren.
Diese Struktur wird in der Graphentheorie untersucht – einem Teilgebiet der Mathematik, das sich mit Verbindungen und Wegen beschäftigt.
Der Mathematiker Leonhard Euler (1707–1783) bewies, dass eine Figur genau dann „in einem Zug“ gezeichnet werden kann, wenn genau zwei Punkte eine ungerade Zahl an Verbindungen haben. Beim Haus vom Nikolaus sind das die beiden unteren Ecken. Genau dort, wo der Stift ansetzt und schließlich wieder absetzt. Man spricht hier von einem sog. Eulerweg.
Warum du das Haus vom Nikolaus nur an zwei Punkten starten kannst
Das erklärt auch, warum du das Haus vom Nikolaus nicht einfach irgendwo beginnen kannst. Startest du an einem anderen Punkt, zum Beispiel am Dach oder an einer Dachkante, dann landest du sicher früher oder später in einer Sackgasse: Es bleibt immer eine Linie übrig, die du nicht mehr ohne Absetzen erreichen kannst.
Nur die beiden unteren Ecken des Hauses haben jeweils drei Verbindungen, also eine ungerade Zahl an Linien. Und genau das ist entscheidend: Nur Punkte mit einer ungeraden Anzahl von Verbindungen können der Start- oder der Endpunkt eines Eulerwegs sein.
Startest du also unten links, musst du unten rechts enden, oder umgekehrt (Startpunkt unten rechts und der Endpunkt dann unten links). Alle anderen Startpunkte führen zwangsläufig zu einem unvollständigen Haus.
Wie viele Möglichkeiten gibt es?
Wenn man das Haus vom Nikolaus in einem Zug zeichnet, also so wie wir es gerade gemacht haben, wie viele verschiedene Wege gibt es dann eigentlich? Nur den Weg, den wir gemacht haben?
Zuerst könnte man denken: nur eine einzige Möglichkeit. Oder vielleicht zwei, wenn man spiegelverkehrt vorgeht. Doch die Mathematik zeigt, dass es viel mehr Varianten gibt, als man erwartet.
Tatsächlich existieren ganze 44 verschiedene Wege, das Haus vom Nikolaus in einem Zug zu zeichnen. Also 44 sogenannte Eulerwege. Berücksichtigt man zusätzlich die gespiegelten Varianten kommt man sogar auf 88 Möglichkeiten.
Was bedeutet „gespiegelt“ in diesem Zusammenhang eigentlich?
Man kann sich das vorstellen wie ein Haus, das im Spiegel betrachtet wird: Die Linien verlaufen in derselben Reihenfolge, aber in umgekehrter Richtung – quasi die „linke“ und die „rechte“ Version des gleichen Weges.
Warum man in der Regel unten startet, hat ebenfalls einen mathematischen Grund:
Nur die beiden unteren Punkte des Hauses haben eine ungerade Anzahl von Verbindungslinien (jeweils drei: Basis, Seitenwand und Diagonale). Das sind die einzigen Punkte, an denen ein Eulerweg beginnen oder enden darf.
Würde man an der Dachspitze (zwei Verbindungslinien) oder an einer Giebelecke (vier Verbindungslinien) starten, käme man unweigerlich in eine Sackgasse. Das Haus ließe sich dann nicht mehr in einem Zug vollenden.
Diese einfache Beobachtung verbindet Zeichnen und Mathematik auf eine faszinierende Weise: Was wie ein Kinderspiel aussieht, folgt einer klaren, logischen Struktur, die Leonhard Euler schon im 18. Jahrhundert beschrieben hat.
Das Haus vom Nikolaus in Aktion
Nachdem wir uns jetzt die Theorie angeschaut haben, wird es Zeit für die Praxis.
Wie sieht das Ganze eigentlich in Bewegung aus?
In unserem YouTube-Short zeigen wir, wie das Haus vom Nikolaus Schritt für Schritt also Linie für Linie entsteht. Natürlich ohne den Stift abzusetzen oder das Video zu schneiden.
So wird sichtbar, wie aus einem vermeintlich einfachen Rätsel ein kleines Stück angewandte Mathematik wird.
Übrigens: Schon 55.000 Nutzer bei YouTube waren neugierig und haben sich angeschaut, wie denn das Haus vom Nikolaus entsteht.
Das Haus vom Nikolaus
🎬 Mehr Mathe in Bewegung?
Hier geht’s zu unserem YouTube-Kanal
💡 Tipp: Wer genau hinschaut, erkennt im Video nicht nur den Zeichenweg, sondern auch, warum die Reihenfolge so entscheidend ist.
Fazit: Das Haus vom Nikolaus neu betrachtet
Wer also am Nikolaustag, dem 6. Dezember, das Haus vom Nikolaus zeichnet, löst –meist ohne es zu wissen – eins klassische Mathematikaufgabe, die bis ins 18. Jahrhundert zurückreicht.
Hinter den scheinbar einfachen Linien steckt ein Stück Graphentheorie und ein Prinzip, das Leonhard Euler erstmals beschrieben hat. Ein Beweis dafür, dass Mathematik oft genau dort steckt, wo man sie am wenigsten vermutet und dass sie, wenn sie richtig erklärt wird, plötzlich ganz einfach und nahbar wirkt.
Diese kleine Zeichnung ist also mehr als nur ein Zeitvertreib aus der Schulzeit.
Sie zeigt, wie man mit mathematischem Denken Ordnung in scheinbares Chaos bringen kann und dass hinter jeder Linie ein Prinzip steckt.
Und genau das ist es, was wir bei der mathe-spezialist® täglich tun:
Wir machen Mathematik nicht magisch, sondern verständlich so, dass sie funktioniert und dich weiterbringt.
Neu auf YouTube: Das Haus vom Nikolaus ausführlich erklärt 🎥
Unser YouTube-Short zum Haus vom Nikolaus hat inzwischen 60.000 Aufrufe erreicht – vielen Dank dafür 🙏!
Und weil so viele wissen wollten, wie genau das funktioniert, gibt es das Rätsel jetzt auch in ausführlicher Form in einem neuen YouTube Video:
FAQ zum Haus vom Nikolaus
Das „Haus vom Nikolaus“ ist eine bekannte Zeichnung aus fünf Punkten und acht Linien, die so verbunden werden, dass ein kleines Haus entsteht. Die Herausforderung besteht darin, das Haus in einem Zug zu zeichnen, ohne den Stift abzusetzen und ohne eine Linie doppelt zu ziehen. Dieses einfache Rätsel wird oft im Mathematikunterricht verwendet, um logisches Denken und geometrisches Verständnis zu fördern.
Hinter der Zeichnung steckt ein mathematisches Prinzip aus der Graphentheorie, das auf den Mathematiker Leonhard Euler zurückgeht. Das Haus vom Nikolaus lässt sich als sogenannter Eulerweg darstellen. Also ein Weg, der jede Kante genau einmal nutzt. Die Struktur des Hauses hat genau zwei Punkte mit ungerader Verbindung, und deshalb kann man es in einem Zug zeichnen, wenn man an einem dieser Punkte startet.
Mathematisch betrachtet existieren 44 verschiedene Möglichkeiten, das Haus vom Nikolaus in einem Zug zu zeichnen. Wenn man die gespiegelten Varianten mitzählt, ergeben sich sogar 88 Wege. Diese Vielfalt zeigt, dass selbst ein scheinbar einfaches Rätsel komplexe mathematische Strukturen enthalten kann.
Ein Eulerweg ist ein Weg in einem Graphen, der jede Kante genau einmal benutzt. Das Haus vom Nikolaus ist ein klassisches Beispiel dafür. Da die Figur genau zwei Ecken mit ungerader Zahl an Verbindungen hat, ist ein solcher Weg möglich. Man muss lediglich an einem dieser Punkte starten und am anderen enden. So verbindet das Haus vom Nikolaus spielerisch Mathematik und Logik.
Nein, nicht mit jedem Punkt funktioniert der Start. Ein Eulerweg – also das Zeichnen des Hauses ohne Absetzen und ohne doppelte Linien – ist nur möglich, wenn du an einem der beiden Knoten mit ungerader Verbindung beginnst. Startest du an einem anderen Punkt, musst du entweder absetzen oder eine Linie doppelt zeichnen, und damit wäre die Bedingung nicht erfüllt.
-
Stille Nacht, eilige Nacht – Wie Quantenphysik den Weihnachtsmann unterstützt
Wie schafft es der Weihnachtsmann eigentlich, innerhalb von nur 24 Stunden mehrere Millionen von Kinder…
-
So geht das Haus vom Nikolaus
Das Haus vom Nikolaus und was Mathematik damit zu tun hat Fast jeder hat es…
Schreibe einen Kommentar